نپسو آژانس دیجیتال

نسبت طلایی مقیاسی است که هر طراحی می بایستی آن را بشناسد. ما توضیح خواهیم داد که این نسبت چیست و چگونه می توانید از آن استفاده کنید.
نوعی نسبت ریاضیاتی معمول در طبیعت قابل یافت است که می توانید از آن برای خلق ترکیبات بصری خوشایند و طبیعی در کارهای طراحی تان استفاده کنید. ما آن را نسبت طلایی می نامیم، ولی با این حال، از این نسبت تحت عناوینی نظیر میانه ی طلایی، برش طلایی و یا حرف فی یونانی نیز یاد می شود. چنانچه شما یک نقاش، یا طراح صحنه و یا طراح گرافیک باشید، مد نظر قرار دادن نسبت طلایی در هر پروژه ای برایتان ارزشمند خواهد بود.
ما در این مقاله به تشریح چیستی این نسبت و نحوه ی استفاده از آن خواهیم پرداخت و به برخی از منابع بسیار عالی جهت مطالعه و دریافت الهامات بیشتر در این رابطه اشاره خواهیم کرد.

نسبت طلایی چیست؟

نسبت طلایی تا حد زیادی به دنباله­ ی فیبوناچیمربوط می ­شود (یعنی همان دنباله­ای که ممکن است آن را از درس­های ریاضی دوران مدرسه و یا از رمان «کد داوینچی» دن براون به یاد داشته باشید) و توضیح­ دهنده ­ی نوعی رابطه ­ی تقارنی عالی و کامل در میان دو بخش است.

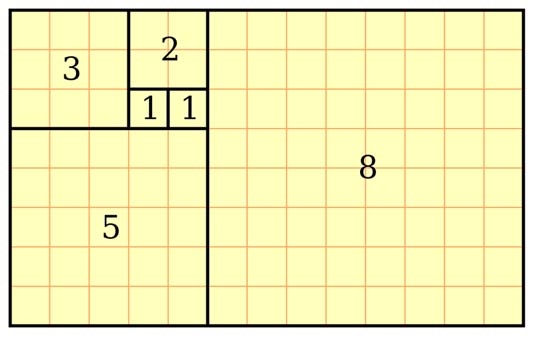
این نسبت طلایی که مقدارش حدوداً معادل 1 به 1/61 است، با استفاده از یک مستطیل طلایی قابل ترسیم خواهد بود: یک مستطیل بزرگ که از یک مربع (با طول اضلاعی برابر با کوچکترین ضلع مستطیل) و یک مستطیل کوچک­ اندازه ­تر تشکیل می ­یابد.

چنانچه این مربع را از درون مستطیل اولیه حذف کنید، یک مستطیل طلایی کوچکتر برای شما باقی خواهد ماند. شما می­ توانید همین کار را به مانند توالی اعداد فیبوناچی ولی در جهت معکوس آن بارها و بارها تا حدی نامتناهی تکرار کنید (افزودن یک مربع با طول ضلع برابر با کوچکترین ضلع مستطیل، حذف بخش مربعی و تکرار مجدد این کار در بخش مستطیلی باقیمانده، شما را بیشتر و بیشتر به دستیابی به مستطیل طلایی و نسبت طلایی نزدیک خواهد ساخت)

استفاده از نسبت طلایی

باور بر آن است که نسبت طلایی برای دورانی به مدت حداقل 4000 سال در زمینه ­ی هنر و طراحی بشر استفاده گردیده است، ولی این زمان می­ تواند حتی از این مدت نیز بیشتر بوده باشد، زیرا که برخی از افراد مدعی آن هستند که حتی مصریان باستان نیز از همین اصل برای ساخت اهرام­شان استفاده کرده بودند.

در زمان­های نزدیک تر به دوران معاصر، شما می­توانید نسبت طلایی را در زمینه­ ی موسیقی، هنر و طراحی در تمامی مکان­های دور و اطراف خودتان مشاهده کنید. شما نیز می­ توانید با استفاده از شیوه­ های مشابه، همین حساسیت ­های طراحانه را به کارهای خودتان بیافزایید.

معماری یونان

معماری یونان باستان از نسبت طلایی برای تعیین نسبت­های ابعادی خوشایند در میان پهنای یک ساختمان و ارتفاع آن و اندازه ­ی ایوان یا سرسرا و حتی تعیین موقعیت ستون­ های نگهدارنده ­ی سازه استفاده می­کرد.

نتیجه­ ی نهایی استفاده از این شیوه، دستیابی به بنایی است که حسی از تناسب کامل را به بیننده القا می­ کند. جنبش معماری نئوکلاسیک نیز بعدها مجدداً به استفاده از همین اصول پرداخت.

 

شام آخر

لئوناردو داوینچی نیز به مانند بسیاری از هنرمندان قرون و اعصار مختلف، برای خلق ترکیب ­بندی ­های خوشایند، به طرز گسترده­ای از نسبت طلایی در کارهایش استفاده کرده است.

در نقاشی شام آخر داوینچی، پیکرهای انسانی در دو-سوم پایینی تصویر (یعنی قطعه­ ی بزرگتر دو بخش مرتبط با نسبت طلایی) چیدمان گردیده ­اند، و موقعیت عیسی مسیح به کامل ترین شکلی از طریق چیدمان مستطیل ­های طلایی در تمام سطح پرده­ ی نقاشی ترسیم گردیده است.

 

طبیعت

همچنین، مثال­ های متعددی نیز از برقراری نسبت طلایی در طبیعت وجود دارند و شما می­ توانید در تمامی مکان­ های پیرامون خودتان این نسبت را مشاهده کنید. گل­ها، صدف­های دریایی، میوه ­های آناناس و حتی چیدمان شانه­ های عسل همه و همه نشانگر نسبت مبنایی یکسانی در ترکیب­بندی و ساختارشان هستند.

بنابراین، استفاده از نسبت طلایی در کار طراحی­ تان، هم با محیط پیرامونی­ مان در تناسب است و هم به شکلی بازنمود دهنده­ ی آن است.

استفاده از نسبت طلایی بسیار ساده­ تر از آن چیزی است که شاید تصورش را بکنید. چند ترفند سریع و راحت وجود دارند که می­ توانید از آن­ها در طرح ­بندی­ هاتان استفاده کنید، و یا می­ توانید قدری بیشتر درباره­ ی آن تدبیر کنید و این مفهوم را به شکلی کامل تر در کارهاتان بگنجانید.

 

http://www.pnidea.com/golden-ratio-fibonacci.html